GEODESIE
Principe et définition
La géodésie est la science des formes et dimensions de la Terre et de son champ de pesanteur.
Elle a deux buts principaux :
• Un but scientifique : contribuer à l´étude de la forme, de la dimension, des déformations et du champ de pesanteur de la terre ;
• Un but utilitaire : déterminer avec le plus de précision possible les coordonnées d´un certain nombre de points géodésiques, servant de charpente et d´ossature aux levées topographiques.
Tous les autres mesurages faits sur la surface de la terre appartiennent aux travaux d´arpentage et travaux topographiques
Géodésie géométrique
Des coordonnées géographiques seules ne veulent absolument rien dire si le système géodésique auquel elles se rapportent n’est pas spécifié.
Un système géodésique est un système de référence permettant d’exprimer les positions sur terre.
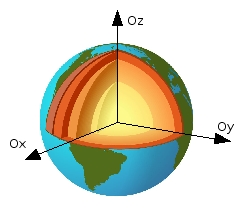
C’est en fait un repère tridimensionnel dont l’origine O se situe au centre des masses de la Terre, ses deux premiers axes sont dans le plan de l’équateur et le 3eme est proche de l’axe de rotation des pôles.
D’autre part, la Terre n’est pas ronde car elle est aplatie aux pôles et sa surface n’est pas régulière. Elle se nome la surface topographique.
Cette surface n’est pas définissable mathématiquement car trop complexe.
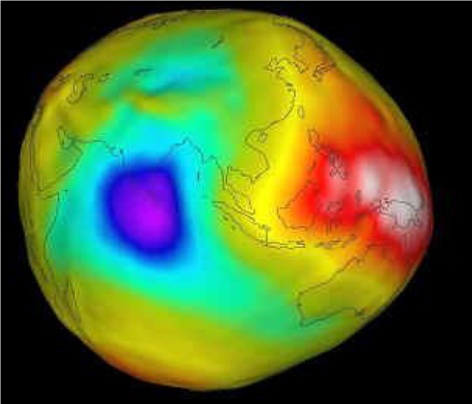
De nombreuses études se sont penchées sur la forme exacte de la Terre.
Il en résulte une surface appelé le géoïde qui se définit comme la surface équipotentielle du champ de pesanteur correspondant au niveau moyen des mers.
Le Géoïde n’est toujours pas définissable mathématiquement pour le calcul de réseaux planimétriques.
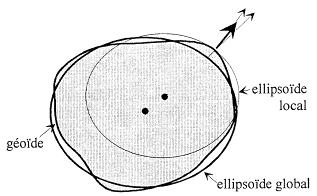
Les surfaces
Comme nous l’avons décrit précédemment, la terre n’est pas plate, ni ronde, ni ellipsoïdale et encore moins régulière.
Afin de nous permettre de projeter un système de coordonnée cohérent, il est nécessaire de modéliser sa surface de façon à ce quelle soit définissable mathématiquement.
Plusieurs types surfaces sont à considérer lorsque l’on s’intéresse au positionnement géodésique :
la surface topographique : (surface réelle de la terre)
le géoïde : surface équipotentielle du champ de pesanteur permettant la modélisation physique de la forme de la terre par rapport à son champ de pesanteur et l’établissement des réseaux qui ceinturent la Terre pour donner un positionnement absolu et relatif en coordonnées géocentriques du niveau moyen des mers.
l’ellipsoïde : surface de type ellipsoïde parfaite passant par un certain nombre de points de référence du géoïde.
La surface topographique
C’est la surface physique de séparation Terre solide – atmosphère. C´est une surface complexe, non modélisable.
Le géoïde
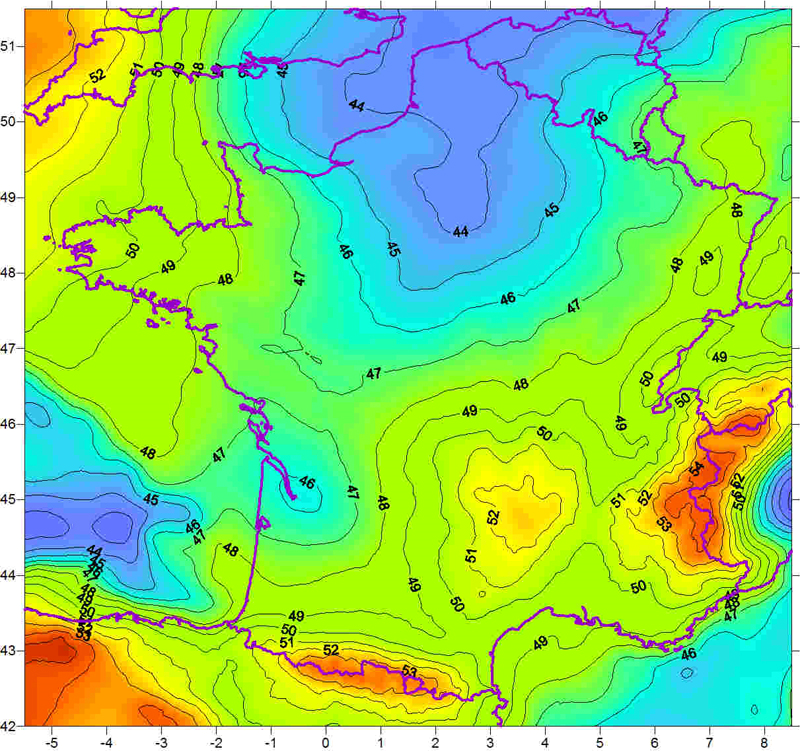
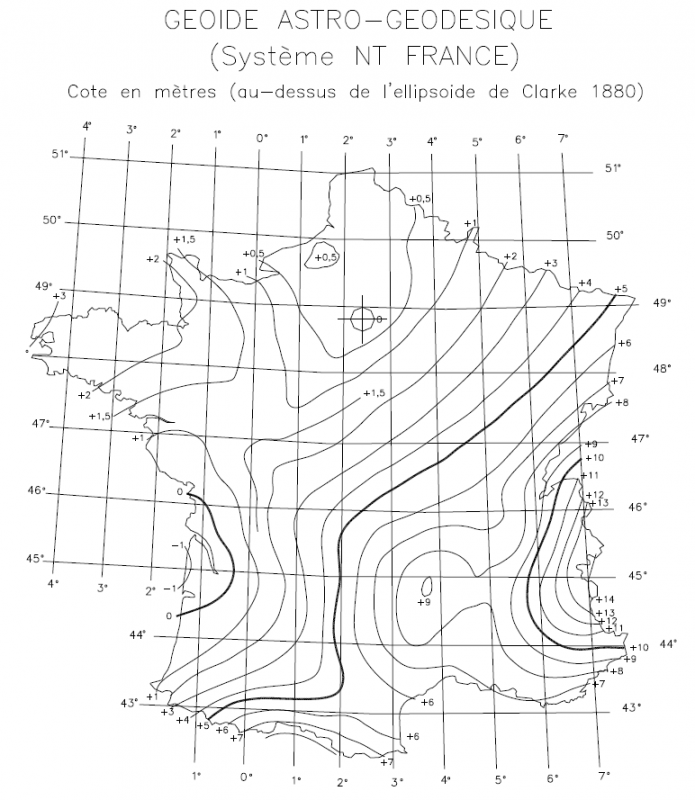
Elle se définit comme la surface équipotentielle du champ de pesanteur correspondant au niveau moyen des mers. Le géoïde français est rattaché au point fondamental de Marseille.
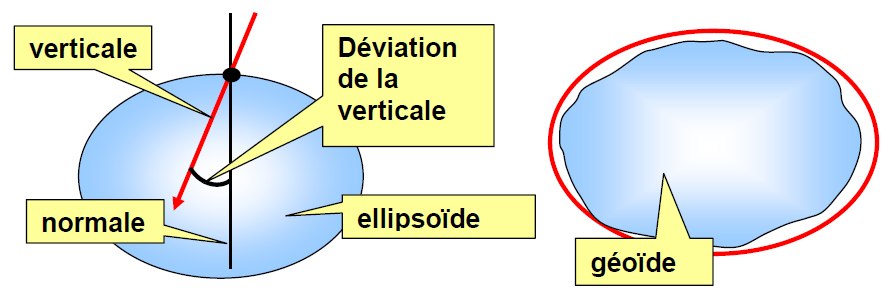
La direction du fil à plomb donne la verticale.
Cette verticale résulte de la force centrifuge de la terre et de la gravité, en un lieu donné.
L’horizontale est par définition perpendiculaire à la verticale !
Du fait des masses voisines plus ou moins hétérogènes, la direction de la verticale n’est pas régulière sur la surface de la terre en raison de l’attraction des masses montagneuses voisines.
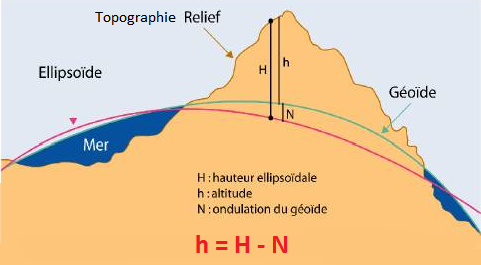
Les systèmes de référence altimétrique
Le développement rapide de l’utilisation du GPS a suscité de nouveaux besoins en matière de systèmes de référence et de conversions de coordonnées, en particulier dans le domaine de l’altimétrie. Alors qu’en géodésie traditionnelle on sépare les déterminations planimétriques et altimétriques, le GPS permet d’intégrer ces opérations. Il devient dès lors nécessaire de convertir les hauteurs ellipsoïdales en altitudes.
Le Service de géodésie et nivellement diffuse des grilles de quasi-géoïde résultant des travaux de développement et de recherche ainsi que des surfaces de conversion d’altitudes directement utilisables pour une estimation de l’altimétrie par GPS :
- Surface de conversion altimétrique RAC09 pour la Corse (IGN78)
- Surface de conversion altimétrique RAF09 pour la France continentale (IGN69)
En France le Géoïde est situé entre 43m et 55m au dessus de l’ellipsoïde.
L’ellipsoïde de révolution
Modèle mathématique défini pour permettre l’application de formules mathématiques pour le calcul de réseaux planimétriques.
Pour qu’il soit le plus près possible du géoïde, il peut être local ou global, selon le champ d’application souhaité du système géodésique auquel il est associé (couverture mondiale ou d’un territoire seulement).
Ellipsoïde 1 = local, Ellipsoïde 2 = local
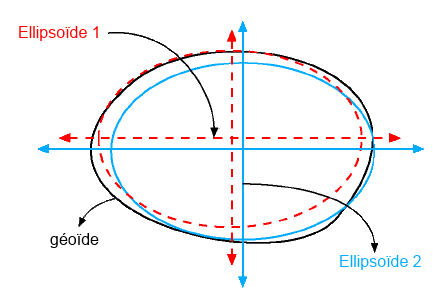
Ellipsoïde global.
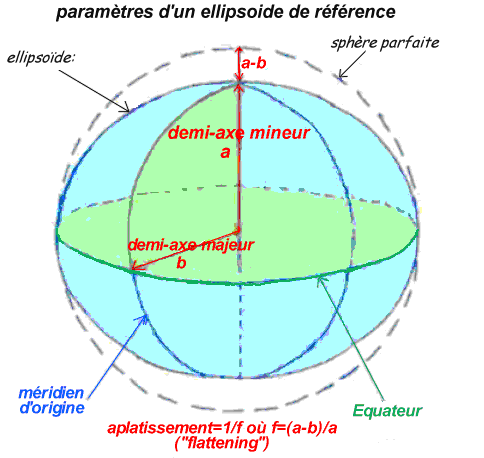
Il n’existe pas un ellipsoïde global unique mais plusieurs ellipsoïdes locaux définis dans chaque pays par rapport aux géoïdes.
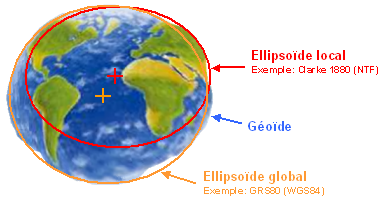
- Ellipsoïde Clarke 1880 (utilisé pour le réseau NTF et systèmes de coordonnées Lambert zones)
- Ellipsoïde Hayford 1909 (utilisé pour le réseau UTM universel Mercator)
- Ellipsoïde IAGRS 1980 (utilisé pour les nouveaux réseaux WGS 84 et RGF 93 et systèmes de coordonnées Lambert 93 et Lambert 9 zones)
Réseau Géodésique
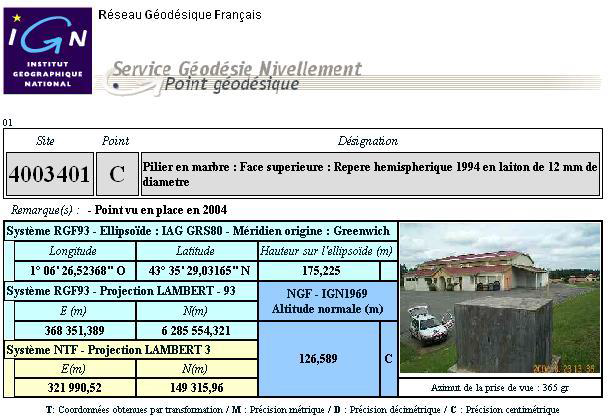
Pour appuyer son système de coordonnées l’IGN a donc implanté en France un réseau de points dits « géodésiques » autrefois appelé La NTF (nouvelle triangulation française 1873-1991). Nous travaillons actuellement avec un nouveau système de référence : le RGF 93.
Ce système appelé Réseau Géodésique Français 1993 (RGF 93) est spatial, tridimensionnel et géocentrique.
Il s’agit d’un réseau de bornes implantées sur le territoire français et qui nous permettent de vérifier, étalonner nos appareils de mesure. Ces bornes ont une précision plus ou moins grande suivant leur classification.
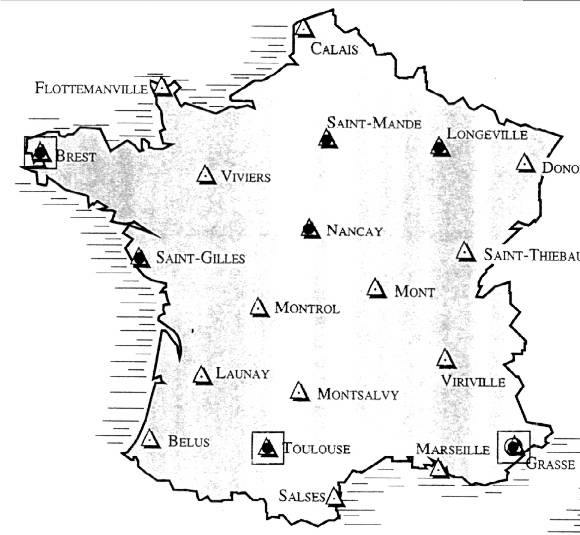
Le système RGF 93 est fondé sur le système mondial WGS 84 (IAGRS 80) qui prend en compte les déformations de la croûte terrestre dues à la tectonique des plaques. Il existe 23 points correspondants à cet ordre là sur notre territoire.
La technique d’observation des points du RGF 93 est celle de la mesure satellitaire GPS assurant ainsi une cohérence de niveau centimétrique à l’ensemble des coordonnées.
Les coordonnées sont fournies sous forme :
Longitude, latitude et hauteur ellipsoïdale sur l’ellipsoïde IAGRS 80
Bi dimensionnelle : E et N selon la projection Lambert 93
Ces 23 points sont évidemment insuffisants pour quadriller le territoire il a fallu donc densifier le canevas avec des mesures GPS et des calculs.
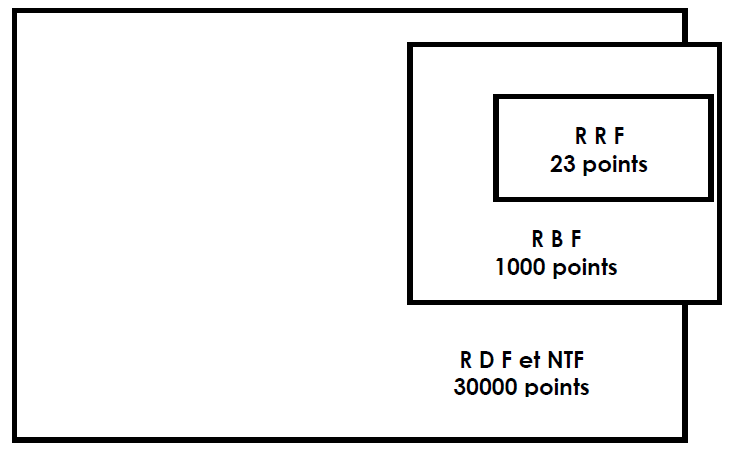
Tout ceci donne la décomposition suivante :
R.R.F : Réseau de Référence Français, basé sur ITRS mondial, 23 points,
R.B.F : Réseau de Base Français, canevas de points observés au GPS, 1000 points
R.D.F : Réseau de Détail Français, canevas de points de la NTF transformés par calcul en RGF 93, 30000 points.
L’ensemble des points géodésiques français sont recensés sur le site geodesie.ign.fr.
On peut éditer la fiche descriptive de chaque point en cliquant information sur un point en cliquant ici.
Différents types de coordonnées
Les coordonnées d’un point peuvent être exprimées de différentes façons
Géographiques : latitude et longitude en valeurs angulaires (ϕ, λ, h)
Ayant pour référence le centre O du système géodésique utilisé, les coordonnées sont déclinées sous forme de 2 angles : latitude et longitude. L’angle 0 de la latitude correspond à l’équateur, et l’angle 0 de la longitude au Méridien de Greenwich.
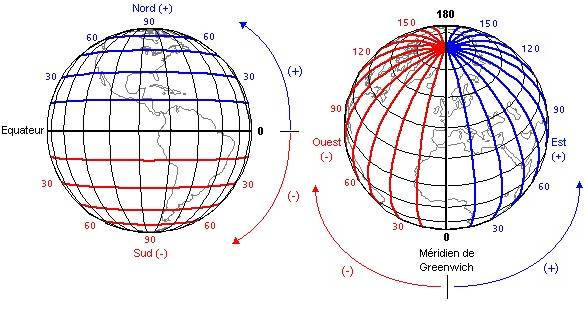
Plusieurs unités d’angle peuvent être utilisées mais les 2 principales sont les degrés décimaux et les degrés sexagésimaux (degré, minute, seconde).
Exemple d’un point situé en France :
En degrés décimaux latitude 45.99972°N – longitude -1.21389°E
En degrés sexagésimaux latitude 45°59’59 »N – longitude 1°12’50 »O
Cartésiennes exprimées dans un référentiel géocentrique en valeurs métriques (X, Y, Z)
Généralement, les coordonnées géocentriques ne servent que d’étape de calcul pour les changements de système géodésique.
En projection : représentation cartographique plane (valeurs métriques non géoréferencées [X, Y] ou géoréferencées [E, N]).
Pour représenter la surface courbe de la Terre sur une surface plate (cartes papiers) il existe différents systèmes de projection de la surface d’un ellipsoïde sur un plan détaillés dans le chapitre suivant.
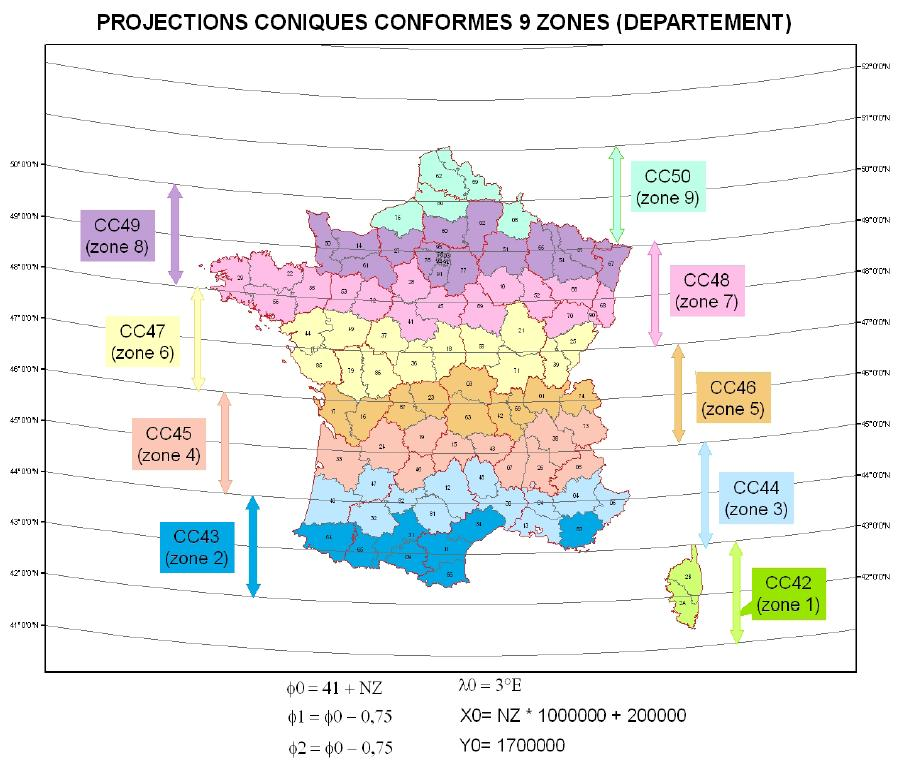
Les systèmes de projection
L’objectif des projections cartographiques est d’obtenir une représentation plane du modèle ellipsoïdal de la surface de la Terre.
Outre le fait qu’une projection plane nous permette d’établir une carte plane facilement utilisable, l’intérêt majeur réside alors dans les valeurs métriques, beaucoup plus facilement exploitables, en particulier pour les mesures de distance.
Mais une projection ne peut jamais se faire sans qu’il y ait de déformations. Néanmoins, par calcul, il est possible de définir le type et les paramètres d’une projection dans le but de minimiser certaines déformations.
On choisit alors :
soit de conserver les surfaces (projection équivalente) altération les longueurs et les angles.
soit de conserver localement les angles (projection conforme) altération des surfaces et des longueurs
soit de conserver les distances à partir d’un point donné (projection équidistante) altération des angles et des surfaces.
Dans tous les cas, aucune projection ne peut conserver toutes les distances. On introduit alors les notions de module linéaire et d’altération linéaire. Aujourd’hui, la plupart des projections utilisées en géodésie et topographie sont conformes. La cartographie à petite échelle utilise souvent des projections équivalentes.
Projections coniques
Dans ce type de représentation, les images des méridiens sont des demi-droites qui concourent en un point image du pôle et les parallèles des arcs de cercles concentriques autour de ce point.
Elles peuvent être réalisées de deux façons :
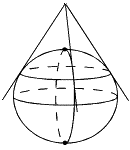 |
TangenteouSécante? |
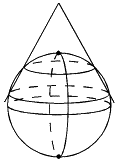 |
| Tangente | Sécante |
Les projections coniques
Projections cylindriques
L’ellipsoïde est projeté sur un cylindre circonscrit le long de l’équateur ou d’un méridien, dans ce cas c’est elle est dite cylindrique transverse. Les zones correctement représentées sont celles proches du méridien de tangence.
Elles peuvent réalisées de trois façons :
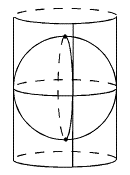
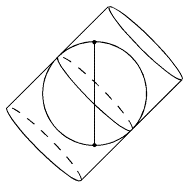
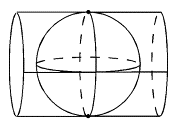
Directe
Oblique
Transverse
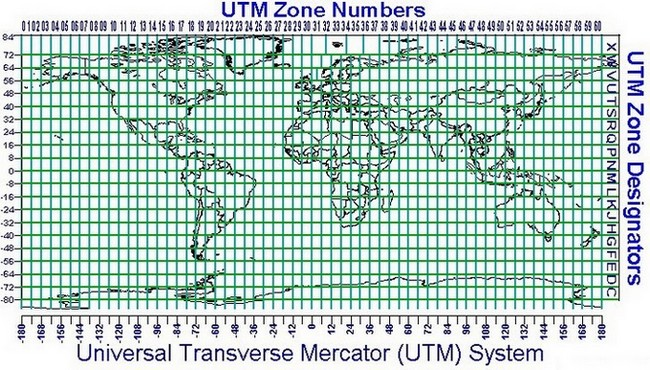
Exemple d’un point situé en France :
Fuseau 31 U = 499991,41 et N = 5608726,34
Autres projections
Il existe encore d’autres types de projection mais leurs utilisations en cartographie sont beaucoup plus spécifiques, voire difficiles, que celles des trois grandes familles qui viennent d’être exposées. C’est pourquoi nous ne nous attarderons pas dessus.
Tableau récapitulatif des systèmes de coordonnées
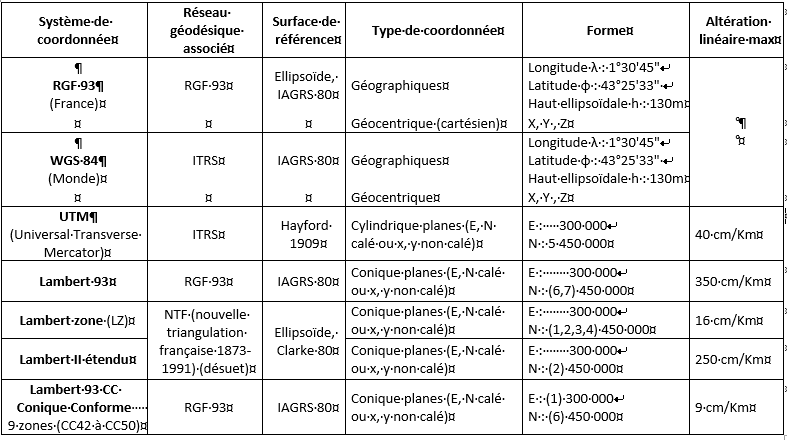
Lexique
Azimut
En topographie, l’azimut d’une direction est l’angle horaire (c’est-à-dire dans le sens des aiguilles d’une montre) compté de 0 à 400 grades, depuis une direction de référence.
Coordonnées géographiques
Position d’un point à la surface de la Terre, définie par une longitude et une latitude. Les coordonnées géographiques découlent d’un système géodésique (cf. définition).
Equidistance des courbes de niveau
Différence d’altitude entre deux courbes de niveau successives.
Géodésie
Science ayant pour but de déterminer la forme et les dimensions de la Terre.
M.N.T.
Modèle Numérique de Terrain.
Traditionnellement en topographie, le modelé d’un terrain est dressé à partir de points caractéristiques remarquables (points hauts ou bas, lignes de ruptures de pentes, …). Ces points, calculés en XYZ, vont composer un semis de points qui correspondront aux sommets des triangles suivant lesquels les interpolations en altitude seront calculées. L’ensemble de ces triangles (ou triangulation) constituera des faces en 3 dimensions et déterminera de manière numérique un modèle du terrain.
Niveau de chantier
Instrument topographique permettant de mesurer des hauteurs ou des différences d’altitudes.
Nord géographique
C’est la direction du méridien d’un point vers le pôle nord. L’angle compris entre le nord géographique et le nord du quadrillage (ou des Y, cf. définition) est appelé convergence des méridiens.
Nord magnétique
C’est la direction de la pointe de l’aiguille aimantée de la boussole, c’est à dire du champ magnétique terrestre du moment et du lieu.
Nord des Y ou nord du quadrillage
C’est la direction de l’axe des Y en un point ; on parle alors de nord U.T.M., nord Lambert,…
Projection cartographique
C’est un ensemble de techniques permettant de représenter la surface plus ou moins sphérique de la Terre dans son ensemble ou en partie sur la surface plane d’une carte ou d’un plan. Les projections conformes conservent les angles (Mercator, Lambert, U.T.M.), les projections équivalentes conservent les surfaces (Bonne, Peters).
Système géodésique
C’est un système de référence permettant d’exprimer les positions au voisinage de la Terre. Les coordonnées géodésiques d’un point dans un système géodésique considéré sont la latitude, la longitude, et la hauteur géodésique. Les systèmes géodésiques les plus connus sont par exemple le W.G.S. 84, la NTF (Nouvelle Triangulation de la France), EUROPE 50, ou ED 50 (pour European Datum 50).
W.G.S. 84
Système de référence géodésique établi par le Service Géographique de l’Armée des U.S.A.