MÉTHODE DE LEVÉ PAR STATION TOTALE
SOMMAIRE
I. PRINCIPE
II. PRECISION
1) La précision ou l’imprécision
2) Combattre l’imprécision
III. TRAITEMENT DES DISTANCES
IV. PRINCIPES D’UN LEVE TOPO
1) Station et mise en station
2) Points rayonnés
3) Points de référence connus
4) Polygonale
a) Polygonale « ouverte »
b) Polygonale « fermée »
V. METHODE DE MISE EN STATION
1) Description
2) Préparation
3) Centrage
4) Quasi-verticalité
5) Verticalité fine – direction VC1-VC2
6) Rotation de l’alidade
7) Verticalité fine – direction VC3
VI. MÉTHODES DE LEVÉ
1) Station « classique »
2) Station libre
3) Méthode mixte : GNSS+station topo
4) Station locale
5) Cheminement de stations
VII. PRÉCAUTIONS ET OBLIGATIONS
VIII. CONSEILS
LEXIQUE
I. Principe
Matériel à visée optique appelé tachéomètre ou station totale

Le tachéomètre est un théodolite, mesurant en plus les distances.
La mesure des distances se fait grâce à un télémètre à visée infrarouge intégré dans le tachéomètre. La mesure se fait à l’aide d’un prisme réflecteur, placé à la verticale du point que l’on souhaite mesurer à l’aide d’une nivelle sphérique. La mesure peut être effectuée au laser avec le même système réflecteur, et même sans réflecteur, ce qui permet de collecter des mesures de points inaccessibles.

Un théodolite est un appareil servant à mesurer les angles horizontaux et verticaux pour déterminer des directions. Il est composé d’une lunette montée sur les deux axes vertical et horizontal. Chacun des axes est équipé d’un cercle gradué permettant les lectures des angles. Le théodolite se pose sur un support et doit être calé sur le plan horizontal à l’aide des nivelles. Il est souvent placé sur un trépied, et à la verticale exacte d’un point connu en coordonnées. L’ensemble de cette phase d’utilisation se nomme « la mise en station ».
La visée se fait à travers la lunette par l’opérateur de visée qui pointe une mire tenue par un autre opérateur.
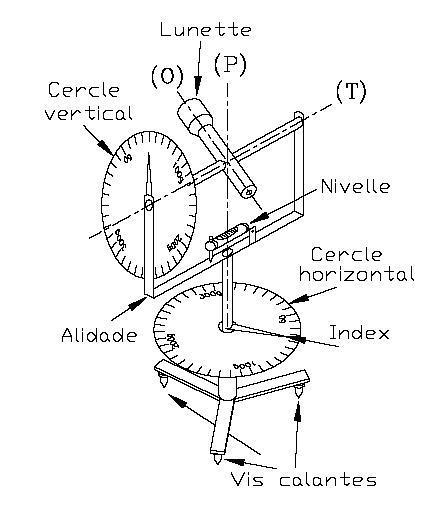
Les parties qui le constituent :
Le cercle horizontal (ou limbe) est la graduation du théodolite sur laquelle l’opérateur lit les angles horizontaux. Il est lié au socle de l’appareil mais peut aussi pivoter sur lui-même de manière à régler le zéro des graduations sur une direction donnée.
Les graduations sont croissantes de 0 à 400 gon dans le sens horaire.
Après la mise en station du théodolite, ce cercle est horizontal, ce qui explique que les angles lus soient des angles projetés sur le plan horizontal et appelés angles horizontaux (ou azimutaux), notés Hz.
Matériel à visée optique appelé tachéomètre ou station totale
Les outils du géomètre profitent constamment des progrès technologiques. Le théodolite, instrument quasi emblématique de la profession, n’échappe pas à cette règle. Dans un premier temps mécano-optique, cet instrument est pourvu d’un nombre grandissant de composants électroniques pour un gain croissant en termes de productivité.
Certains tachéomètres sont équipés de servomoteurs, permettant de diriger automatiquement leur lunette dans n’importe quelle direction. Le procédé de localisation automatique du réflecteur permet de diriger automatiquement l’instrument sur le prisme.
Là encore un gain croissant de productivité car l’opérateur est désormais seul à travailler sur le chantier. Il doit tenir le réflecteur et un module d’enregistrement. La liaison entre ces deux composantes s’effectue par ondes radio ou par Bluetooth.

II. Précision
1) La précision ou l’imprécision
La précision ou l’imprécision engendrée par ce type de solution dépend de différents facteurs :
- Du matériel : chaque appareil justifie d’une précision de mesure
- De la mise en œuvre lors de l’utilisation de l’appareil, pendant le calage de la station de travail ainsi qu’au moment de la prise de la mesure.
- Des conditions : la réfraction et la température ainsi que le vent, le soleil et les vibrations peuvent influencer sur les résultats de façon significative et jouer un rôle perturbateur important. On peut observer par exemple un doublement ou triplement des valeurs de précision nominales de l’appareil.
- Du système de coordonnées utilisé
2) Combattre l’imprécision
Comment la combattre l’imprécision :
Les limitations de conditions de levé sont liées aux conditions atmosphériques, distance, portée Bluetooth et peuvent jouer un rôle plus ou moins important sur l’imprécision d’une mesure ou d’un levé. Parmi les précautions d’usage que l’on peut citer :
Entretenir son matériel de façon rigoureuse, humidité, condensation, poussière.
Faire contrôler son matériel tous les ans.
Mettre en œuvre des opérations de contrôle durant le levé du chantier (visée systématique de point ayant déjà été levé avant changement de station ou visée de point déjà acquis tous les 50 points)
Utiliser les principes de la compensation de l’erreur par double retournement pour les mesures de points éloignés.
Compensation par cheminement/polygonale (ouvert, fermé).
Plus généralement, nous pouvons admettre que les facteurs générant de l’imprécision dans ce type de mesure, levé ou repérage, sont maitrisables pour la plupart ou contournables par des opérations de contrôle et de doubles ou triples mesures par double retournement.
III. Traitement des distances
En fait, une distance, mesurée sur le terrain, doit subir quelques traitements numériques avant d’être introduite dans les calculs (ou reportée sur un plan).
L’exactitude de la visée laser doit être compensée par différents types de corrections liées à des phénomènes optiques et atmosphériques.
Le report d’une mesure 3 dimensions avec un dénivelé sur un plan en 2 dimensions nécessite également une correction.
Le fait d’utiliser un système de coordonnées projeté nécessite là encore une correction spécifique par rapport à l’emplacement géographique du levé et au système choisi.
L’ensemble de ces étapes s’appelle « le traitement des distances
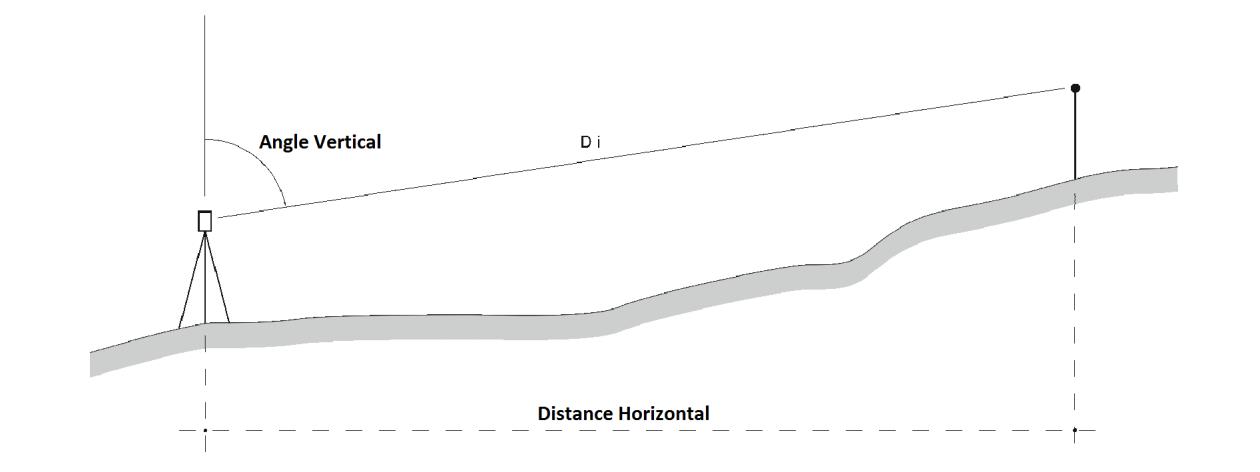
Réduction à l’horizontale
La distance inclinée est celle mesurée sur le terrain (suivant l’axe distance-mètre /réflecteur). La distance réduite à l’horizontale est celle séparant réellement deux points : c’est donc celle reportée sur le plan.
Dh = Di x sin(Av) (Cette réduction est particulière à chaque mesure)
La correction de représentation plane ou de projection.
Nous traiterons ici la correction de réduction à la projection plane du système de coordonnée utilisé.
Kf est le coefficient d’altération linéaire, il est donné dans l’abaque de L’IGN
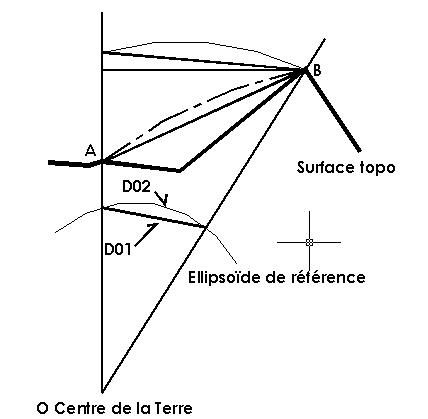
Réduction à l’ellipsoïde
Do = (Dh x R) / (R + h) avec h = hauteur ellipsoïdale relative à la projection du point visé sur la verticale passant par la station. (Cette réduction est particulière à chaque visée en zone montagneuse, par contre, en plaine, on peut adopter un module commun au chantier, m = R / (R + h), pour déduire Do = Dh x m )
Correction du Niveau apparent
En nivellement indirect parfois les portées peuvent être importantes, à partir de 500 m il faudra prendre en compte dans l’exploitation des données deux erreurs systématiques :
L’erreur due à la sphéricité de la Terre
L’erreur due à la réfraction terrestre
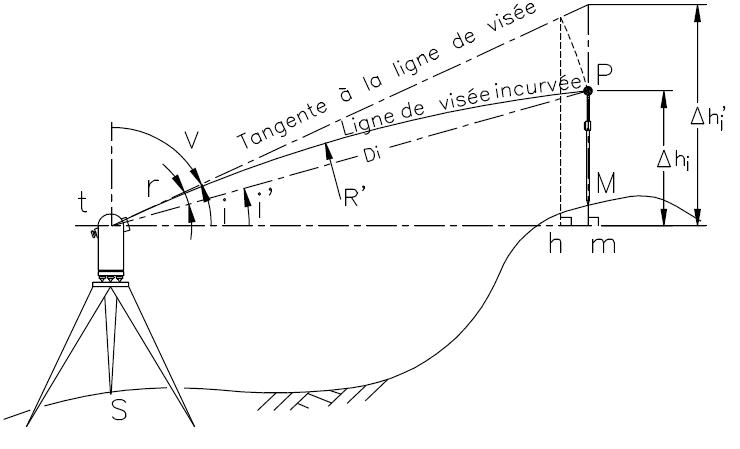
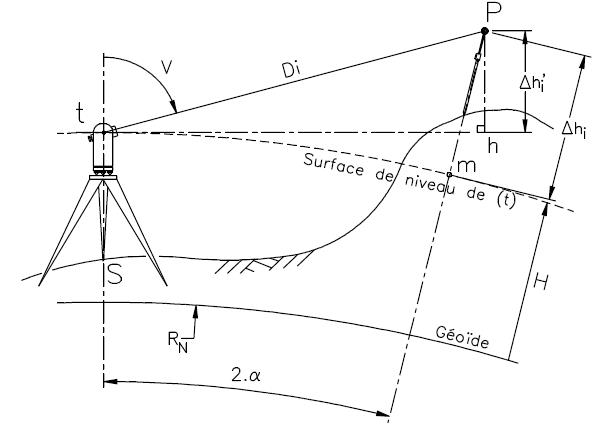
Les surfaces de niveaux ne sont pas planes et localement assimilables à des sphères de rayon Rn + H (alt). Cela induit deux types d’erreurs :
L’erreur sur la dénivelée instrumentale
L’erreur sur la distance horizontale
Le trajet optique du rayon lumineux du tachéomètre n’est pas linéaire mais incurvé vers la surface terrestre du fait de la réfraction atmosphérique. L’angle de déviation ou de réfraction r est fonction de la pression et de la température.
Chacune de ces erreurs peut être corrigée séparément néanmoins il existe une correction globale, toujours positive, qui sera appliquée à la dénivelée : la Correction du Niveau apparent (CNA).
Cna = Dh² (avec Cna en mètre, et Dh en km)
15.2
Exemple : Cna =0.7mm à 100m, 2mm à 200m et 1.6cm à 500m
NB : il est à noter que le flamboiement de l’air du à la surchauffe du sol, occasionne un tremblement de l’image que vous percevez. Il est inutile d’essayer d’avoir des mesures précises dans ce cas de figure, il faut éviter les visées en bas de mire près du sol lorsqu’il fait chaud.
[…]

